Posição relativa entre duas retas

Duas retas podem ser representadas em um plano cartesiano de forma paralela ou concorrente. Mas cada uma dessas formas possui características e elementos que ajudam na identificação da forma que estão dispostas no plano, sem ser preciso construir o gráfico.

Considere duas retas distintas do plano cartesiano:

Podemos classificá-las como paralelas ou concorrentes.

Retas Paralelas

As retas r e s têm o mesmo coeficiente angular
r:y=ar+br e
s:y=as+br esntão as retas r e s são paralelas (r//s) e ar=as

Retas Concorrentes

As retas r e s têm coeficientes angulares diferentes.

Dadas as retas  r: y= ar+br e

                          s:y=as+bs então as s e r são concorrentes sse e ar ar diferente de as

Retas Perpendiculares

É um caso particular de reta concorrente. Duas retas são ditas perpendiculares quando os seus coeficientes angulares são tais que: r:y=arx + br

                                                          s:y=asx + bs são perpendiculares sse * as ar=-1

Fonte:http://www.infoescola.com/geometria-analitica/posicoes-relativas-de-duas-retas/

Equação geral da reta

Para determinarmos a equação geral de uma reta utilizamos os conceitos relacionados a matrizes. Na determinação da equação na forma ax + by + c = 0 aplicamos a regra de Sarrus utilizada na obtenção do discriminante de uma matriz quadrada de ordem 3 x 3. Para utilizarmos uma matriz nessa determinação da equação feral devemos ter no mínimo dois pares ordenados (x,y) dos possíveis pontos alinhados, por onde a reta irá passar. Observe a matriz geral da determinação da equação geral:



Na matriz temos os pares ordenados que devem ser informados: (x₁, y₁) e (x₂, y₂) e um ponto genérico representado pelo par (x, y). Observe que a 3º coluna da matriz é completada com o algarismo 1. Vamos aplicar esses conceitos na obtenção da equação geral da reta que passa pelos pontos A(1, 2) e B(3,8), veja:
Ponto A temos que: x₁ = 1 e y₁ = 2
Ponto B temos que: x₂ = 3 e y₂ = 8
Ponto genérico C representado pelo par ordenado (x, y)

Calcular o determinante de uma matriz quadrada aplicando a regra de Sarrus significa:

1º passo: repetir a 1º e a 2º coluna da matriz.
2º passo: somar os produtos dos termos da diagonal principal.
3º passo: somar os produtos dos termos da diagonal secundária.
4º passo: subtrair a soma total dos termos da diagonal principal dos termos da diagonal secundária.

Observe todos os passos na resolução da matriz dos pontos da reta:

(1 * 8 * 1) + (2 * 1 *x) + (1 * 3 * y)] – [(2 * 3 * 1) + (1 * 1 * y) + (1 * 8 * x)] = 0
[ 8 + 2x + 3y] – [6 + y + 8x] = 0
8 + 2x + 3y – 6 – y – 8x = 0
2x – 8x + 3y – y + 8 – 6 = 0
–6x + 2y + 2 = 0

Os pontos A(1, 2) e B(3,8) pertencem a seguinte equação geral da reta: –6x + 2y + 2 = 0.

Atividade do livro 

A(-1,6) B(2,-3)

m= Yb-Ya=  m-3-6=  9/3=  -3/1

      Xb-Xa      2-(-1)

 Y-yo= m (x-xo)

 Y-(-3)= -3/1 (x-2)

 Y+3= -3x/1 - 6/1

 Y=-3-3x/1-6/1

 Y=-3x/1 - 9/1

 -3x/1 - 9/1 - y/1=0

 -3x/1 -9 -y  

Fonte: http://www.brasilescola.com/matematica/equacao-geral-reta.htm

Matemática Contexto e Aplicações Volume 3 

Equação segmentária da reta

O estudo analítico da reta é muito utilizado em problemas cotidianos ligados a diversas áreas do conhecimento, como a física, biologia, química, engenharia e até a medicina. Determinar a equação da reta e compreender seus coeficientes é bastante importante para a compreensão do seu comportamento, sendo possível analisar sua inclinação e os pontos onde intercepta os eixos do plano. Sobre as retas temos os seguintes tipos de equação: equação geral da reta, equação reduzida, equação paramétrica e equação segmentária. Faremos o estudo da equação segmentária da reta e sua utilização.

Considere uma reta s qualquer do plano de equação ax + by = c. Para obtenção da equação segmentária da reta s basta dividir toda a equação por c, obtendo:


Que é a equação na forma segmentária da reta s



Exemplo 1. Determine a forma segmentária da equação da reta s cuja equação geral é:
s: 2x + 3y – 6 = 0
 Solução: Para determinar a equação segmentária da reta s devemos isolar o termo independente c. Assim, segue que:
2x + 3y = 6

Dividindo a equação por 6, obtemos:

A identidade acima é a forma segmentária da equação da reta s.

Fontes:http://www.brasilescola.com/matematica/equacao-segmentaria-reta.htm

Coeficiente angular

A fórmula que será apresentada para facilitar o cálculo do coeficiente angular de uma reta só poderá ser utilizada por retas não-verticais, ou seja, retas onde sua inclinação é maior ou igual a 0° e menor que 180°, sendo diferente de 90°. 
Veja os passos que foram levados em consideração para obter o cálculo do coeficiente angular de uma reta. 
Considere os pontos A(x_A, y_A) e B(y_B, y_B), esses formam uma reta t no plano cartesiano de inclinação α:


Prolongando o segmento de reta que passa pelo ponto A paralelo ao eixo Ox formamos um triângulo retângulo BMA. E um ângulo equivalente ao da inclinação da reta. 

Levando em consideração o triângulo retângulo BMA e o seu ângulo α, teremos como cateto oposto a y_B – y_A e cateto adjacente x_B – x_A. 
Sabendo que: 
• O coeficiente angular de uma reta é o mesmo que a tangente do ângulo de inclinação. 
• A função tangente é calculada pela razão do cateto oposto pelo cateto adjacente. 

Assim, podemos concluir que o coeficiente angular (m) de uma reta será calculado através da seguinte fórmula: 
m = tg α = yB – yA 
                   xB – xA 

Atividade do livro página 59 questão 29

a) A(3,2) B(-3,-1)

m=(-1)-2= -1/2
     -3-3  

b) A(2,-3) B(-4,3)
m= -3-3= -1/6
 -4-2  

c) P1(3,2) P2(3,-2)
m=2-2= não há coeficiente angular
3-3 

d) P1(-1,4) P2(3,2)
m= 2-4=-1/2
 3-(-1)

e)P(5,2) Q(-2,-3)
m=-3-2= 5/7
-2-5 

f)A((200,100) B(300,80)
m= 80-100= 1/5
 -300-200

Fontes:http://www.mundoeducacao.com/matematica/calculo-coeficiente-angular.htm
Matemática Contexto e Aplicações Volume 3 

Ponto médio de um segmento

O segmento de reta é um subconjunto da reta, é parte da reta.
Ao contrário da reta, o segmento é finito, possuindo começo e fim, podendo ser medido. Mesmo sendo finito, ele possui infinitos pontos e o ponto que divide o segmento de reta em duas partes de mesmo tamanho é chamado de ponto médio.



 Vamos determinar as coordenadas do ponto médio do segmento PQ da figura.

 
Assim, o ponto médio tem coordenadas:


Exemplo 1. Determine as coordenadas do ponto médio do segmento AB de extremos A(1, 9) e B(7, 5).
Solução: Temos que:



Atividade do livro página 55

17- Determine o ponto médio dos segmentos:

a)A(-1,7) e B(3,-5)

Xm= 1+3= 4=2     Ym:(-7)-5= 12= 6  
       2      2                    2     2

b)A(-1,5) B(5,-2)

Xm= (-1)+5= 4= 2   Ym=5+(-2)= 3
        2      2                  2    2

c)A(-4,-2) B(-2,-4)

Xm= (-4)+(-2)= -6= 3   Ym=(-2)+(-4)= 6 = 3
        2      2                  2    2


19-A(5,8) B(2,2) C(8,2)


AB- Xm= 5+2= 7        Ym= 8+2= 10= 5
      2      2                 2    2

BC- Xm= 2+8=10=5   Ym= 2+2= 4= 2
      2      2                   2   2

AC- Xm= 5+8=13       Ym= 8+2=10= 5
      2      2                  2   2 

 Fonte: http://www.alunosonline.com.br/matematica/ponto-medio-um-segmento-no-plano.html
Matemática Contexto eAplicações Volume 3

Condição de alinhamento de três pontos

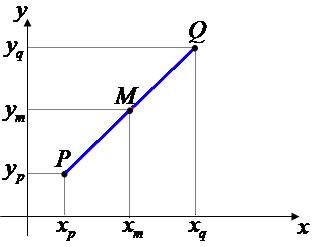
Três pontos estão alinhados se, e somente se, pertencerem à mesma reta.

 Para verificarmos se os pontos estão alinhados, podemos utilizar a construção gráfica determinando os pontos de acordo com suas coordenadas posicionais. Outra forma de determinar o alinhamento dos pontos é através do cálculo do determinante pela regra de Sarrus envolvendo a matriz das coordenadas.

 exemplo 1

Dados os pontos A (2, 5), B (3, 7) e C (5, 11), vamos determinar se estão alinhados.

 

Diagonal principal

2 * 7 * 1 = 14
5 * 1 * 5 = 25
1 * 3 * 11 = 33

Diagonal secundária

1 * 7 * 5 = 35
2 * 1 * 11 = 22
5 * 3 * 1 = 15

 Somatório diagonal principal – Somatório diagonal secundária

(14 + 25 + 33) – (35 + 22 + 15)

72 – 72 = 0
Os pontos somente estarão alinhados se o determinante da matriz quadrada calculado pela regra de Sarrus for igual a 0.

Exemplo 2

Considerando os pontos A(2, 2), B(–3, –1) e C(–3, 1), verifique se eles estão alinhados.


Diagonal principal

2 * (–1) * 1 = –2
2 * 1 * (–3) = –6
1 * (–3) * 1 = –3

Diagonal secundária

1 * (–1) * (–3) = 3
2 * 1 * 1 = 2
2 * (–3) * 1 = –6

(– 2 – 6 – 3) – (3 + 2 – 6)
– 11 – (–1)
– 11 + 1 = – 10

Pelo resultado do determinante da matriz verificamos que os pontos não estão alinhados.

Atividade do livro- Página 57

23- A(0,2) e B(-3,) C(4,5)

0  2  1 1 0  2
-3 1  1 1 -3 1         D= 0+8+(-15)-6-0-4=-17
4  5  1 1  4  5 

obs: Se o alinhamento foi igual a 0 os pontos estão alinhados, tomando a forma de um triângulo, porém se for diferente de 0 não estarão alinhados.

Fontes: http://www.mundoeducacao.com/matematica/condicao-alinhamento-tres-pontos.htm
Matemática Contexto e informações Volume 3

Vídeo: Geometria Analítica

Olá! Demorei mais cheguei. Hoje trouxe uma vídeo aula do professor Jairo que mostra a iniciação da Geometria analítica com técnicas fáceis para descomplicar a sua vida na hora da avaliação. Veja abaixo:

E então? se ligou?! Aguarde novas postagens e bons estudos.
Créditos: aulalivre.net (você pode baixar materiais para estudo nesse site)