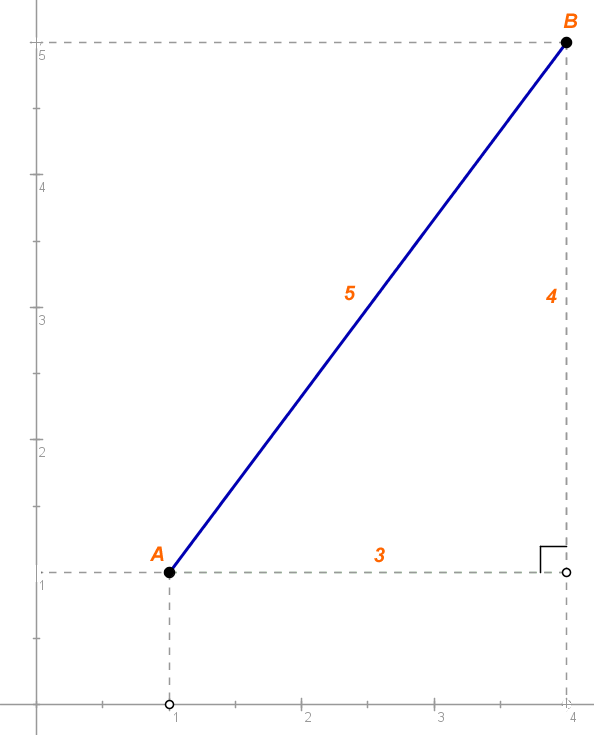
Considere duas retas distintas do plano cartesiano:
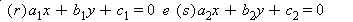
Podemos classificá-las como paralelas ou concorrentes.
Retas Paralelas
As retas r e s têm o mesmo coeficiente angularr:y=ar+br e
s:y=as+br esntão as retas r e s são paralelas (r//s) e ar=as
Retas Concorrentes
As retas r e s têm coeficientes angulares diferentes.
Dadas as retas r: y= ar+br e
s:y=as+bs então as s e r são concorrentes sse e ar ar diferente de as
Retas Perpendiculares
É um caso particular de reta concorrente. Duas retas são ditas perpendiculares quando os seus coeficientes angulares são tais que: r:y=arx + br
s:y=asx + bs são perpendiculares sse * as ar=-1
.jpg)
.jpg)
.jpg)



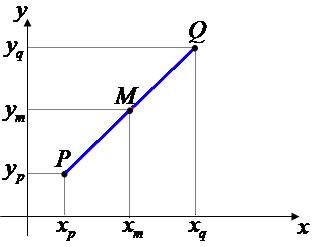
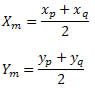




.png)
.png)