Ao contrário da reta, o segmento é finito, possuindo começo e fim, podendo ser medido. Mesmo sendo finito, ele possui infinitos pontos e o ponto que divide o segmento de reta em duas partes de mesmo tamanho é chamado de ponto médio.
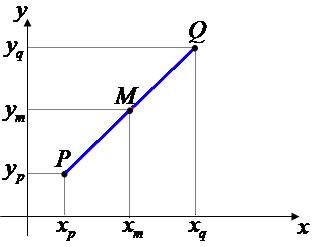
Vamos determinar as coordenadas do ponto médio do segmento PQ da figura.
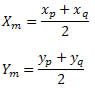
Assim, o ponto médio tem coordenadas:
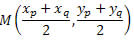
Exemplo 1. Determine as coordenadas do ponto médio do segmento AB de extremos A(1, 9) e B(7, 5).
Solução: Temos que:
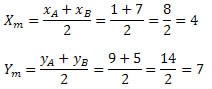
Atividade do livro página 55
17- Determine o ponto médio dos segmentos:
a)A(-1,7) e B(3,-5)
Xm= 1+3= 4=2 Ym:(-7)-5= 12= 6
2 2 2 2
b)A(-1,5) B(5,-2)
Xm= (-1)+5= 4= 2 Ym=5+(-2)= 3
2 2 2 2
c)A(-4,-2) B(-2,-4)
Xm= (-4)+(-2)= -6= 3 Ym=(-2)+(-4)= 6 = 3
2 2 2 2
19-A(5,8) B(2,2) C(8,2)
AB- Xm= 5+2= 7 Ym= 8+2= 10= 5
2 2 2 2
BC- Xm= 2+8=10=5 Ym= 2+2= 4= 2
2 2 2 2
AC- Xm= 5+8=13 Ym= 8+2=10= 5
2 2 2 2
Fonte: http://www.alunosonline.com.br/matematica/ponto-medio-um-segmento-no-plano.html
Matemática Contexto eAplicações Volume 3





0 comentários:
Postar um comentário